布隆过滤器的原理,高效空间利用与概率性数据结构原理解析

你有没有想过，在浩瀚的数据海洋中，如何快速判断一个元素是否存在于某个集合里？传统的哈希表虽然查询速度快，但随着数据量的增长，内存消耗会急剧上升。这时，布隆过滤器（Bloom Filter）就闪亮登场了。它是一种空间效率极高的概率型数据结构，能在极小的空间内完成元素的快速检索，同时保持较低的误判率。今天，就让我们一起深入探索布隆过滤器的原理，看看它是如何做到这一切的。

布隆过滤器的核心组成

布隆过滤器主要由两部分组成：一个位数组和一系列哈希函数。位数组是一个由0和1组成的数组，初始时所有位都设置为0。哈希函数则是一系列将输入映射到位数组特定位置的函数。通常，布隆过滤器会使用多个哈希函数（k个），以确保元素的插入和查询更加均匀和高效。

想象你有一个长长的二进制向量，就像一个巨大的开关矩阵，每个开关初始时都是关闭的（值为0）。同时，你有一把多把不同的钥匙（哈希函数），每把钥匙都能打开向量中的多个开关。当你向布隆过滤器中添加一个元素时，你会用每把钥匙去尝试打开对应的开关，并将这些开关全部打开（设置为1）。查询时，你同样用这些钥匙去检查对应的开关是否都已打开，如果都打开了，就认为元素可能存在；如果任何一个开关是关闭的，就确定元素不存在。

布隆过滤器的插入过程

向布隆过滤器中插入一个元素的过程非常简单。首先，你需要选择k个哈希函数，这些函数会将元素映射到位数组上的k个不同位置。将这k个位置的位都设置为1。这个过程可以重复进行，直到所有需要插入的元素都处理完毕。

以一个简单的例子来说明。假设你有一个长度为8的位数组，并且选择了3个哈希函数。现在，你想要插入一个元素“apple”。第一个哈希函数将“apple”映射到位数组的第2位，第二个哈希函数映射到位数组的第5位，第三个哈希函数映射到位数组的第7位。你将这三个位置的位都设置为1。这样，位数组就变成了00101101。

布隆过滤器的查询过程

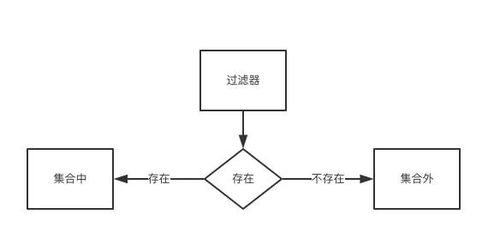
查询一个元素是否存在于布隆过滤器中的过程与插入过程类似。同样地，你需要使用相同的k个哈希函数处理待查元素。如果任意一个由哈希函数产生的索引对应的位仍为0，则可断定此元素一定不属于当前集合；反之，若所有相关位均已被标记为1，则认为该元素可能存在。

继续上面的例子，假设你想要查询元素“apple”是否存在于布隆过滤器中。你同样使用那3个哈希函数，分别得到第2位、第5位和第7位。如果这三个位置的位都是1，那么布隆过滤器认为“apple”可能存在于集合中；如果这三个位置中有任何一个位是0，那么“apple”一定不在集合中。

误判的产生与控制

布隆过滤器的一个主要缺点是存在一定的误判率（False Positive Rate, FPR）。这是由于哈希函数的存在，多个不同的元素可能会映射到位数组的相同位置，导致误判。例如，假设另一个元素“banana”也被插入到了布隆过滤器中，并且它通过哈希函数映射到了与“apple”相同的三个位置。那么，当你查询“apple”时，可能会误判它存在于集合中，尽管实际上它并不存在。

误判率与位数组的长度m、哈希函数的个数k以及布隆过滤器中存入的数据量n有关。当m增大、k增大、n减小时，误判率会降低。因此，在实际应用中，需要根据具体需求调整这些参数，以平衡空间效率和误判率。

布隆过滤器的应用场景

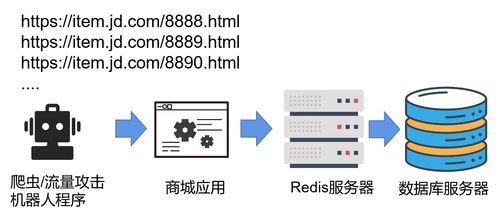
布隆过滤器在许多领域都有广泛的应用，其中最典型的场景之一是解决缓存穿透问题。在缓存系统中，布隆过滤器可以在查询缓存之前快速判断一个数据是否存在，从而避免大量不存在的数据直接穿透缓存访问数据库，减轻数据库的压力。

例如，假设你有一个电商网站，用户经常查询一些不存在的商品。如果没有布隆过滤器，每次查询都会直接访问数据库，导致数据库压力巨大。而有了布隆过滤器，你可以在缓存中设置一个布隆过滤器，当用户查询一个商品时，先在布隆过滤器中判断该商品是否存在。如果存在，再发起对数据库的请求；如果不存在，直接拦截，从而减少数据库的压力。

布隆过滤器的优缺点

布隆过滤器的优点主要体现在以下几个方面：

1. 空间效率高：相比于传统的数据结构（如哈希表），布隆过滤器在存储大规模数据时占用的空间要小得多。因为它