布隆过滤器的误判率是多少,优化策略与实际应用

想象你正在浏览一个巨大的在线图书馆，想要快速找到一本特定的书。你不想浪费时间在那些明显不相关的书籍上，对吧？这时，布隆过滤器就像一位聪明的图书管理员，它能在你开口之前就告诉你：“这本书可能不在我们这里，或者它一定不在。”布隆过滤器是一种神奇的数据结构，它用极小的空间和极快的速度判断一个元素是否可能存在于集合中。但就像任何魔法都有其局限性一样，布隆过滤器也有一个“小缺点”——它可能会“撒谎”，这就是所谓的误判率。那么，布隆过滤器的误判率到底是多少呢？让我们一起深入探索这个话题。

布隆过滤器的奇妙世界

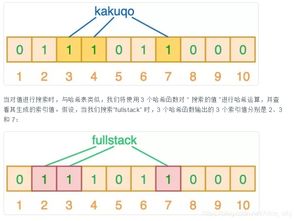
布隆过滤器是由布隆在1970年提出的，它由一个位数组和多个哈希函数组成。位数组就像一个巨大的开关板，每个开关代表一个位，初始时都是关闭的（值为0）。当你向布隆过滤器中添加一个元素时，多个哈希函数会同时工作，将这个元素映射到位数组中的多个位置，并将这些位置的开关打开（设置为1）。查询时，同样的哈希函数会再次工作，检查这些位置是否都打开了。如果都打开了，布隆过滤器认为该元素可能存在；如果任何一个位置是关闭的，它就确定该元素绝对不存在。

布隆过滤器的优点非常明显。它使用空间极小，查询速度极快，适用于大规模数据的快速检索。比如，在网页爬虫中，布隆过滤器可以用来对URL进行去重，避免重复爬取相同的页面；在垃圾邮件识别中，它可以快速判断一封邮件是否可能是垃圾邮件；在数据库查询中，它可以快速判断某个值是否存在于某个字段中，从而避免不必要的全表扫描。

误判率：布隆过滤器的“小缺点”

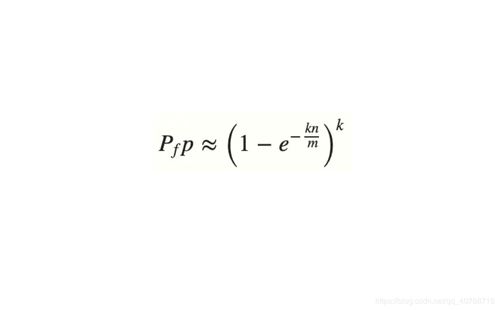
尽管布隆过滤器非常强大，但它也有一个“小缺点”——误判率。由于多个元素可能会通过哈希函数映射到相同的位置，导致位数组中的某些位被错误地置为1，因此在查询时，可能会出现某个元素不在集合中，但由于哈希冲突导致位数组中的位置都为1，从而误判该元素存在。这就是布隆过滤器的误判率。

误判率是布隆过滤器的一个重要参数，它指的是在过滤器中查询一个不存在的元素时，会将其误认为存在的概率，通常用假阳性率（False Positive Rate）来衡量。一个低误判率的过滤器可以减少冗余计算、降低系统开销和提升性能。

误判率是如何计算的？

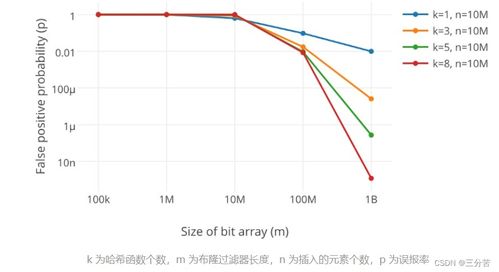
误判率取决于哈希函数的数量与哈希函数的质量。布隆过滤器通常采用单向哈希函数，可以使用多个不同的哈希函数来提升误判率的表现。具体来说，误判率与哈希函数数量、被过滤的元素数量和过滤器的大小有关。

对于单个哈希函数的布隆过滤器，误判率的计算公式如下：

\\[ p = (1 - e^{-kn/m})^k \\]

其中，\\( m \\) 是布隆过滤器的大小（位数组的大小），\\( n \\) 是元素个数，\\( k \\) 是哈希函数个数，\\( p \\) 是误判率。

而对于多哈希函数的布隆过滤器，误判率的计算公式如下：

\\[ p = (1 - 1/m)^{kn} \\]

相比于单哈希函数，多哈希函数的布隆过滤器可以减少误判率，但需要更多的哈希函数和存储空间。

如何控制误判率？

影响误判率的因素有很多，可以通过控制这些因素来控制误判率。

首先，增加过滤器的大小可以减少误判率。当一个元素被哈希到一个比较拥挤的区域时，就有可能与其他元素在同一个位置出现冲突，导致误判。因此，增加位数组的大小可以减少冲突的概率，从而降低误判率。

其次，增加哈希函数的数量也可以降低误判率。哈希函数的数量越多，每个元素在布隆过滤器中对应的位数组位置被置为1的概率就越高，这有助于减少因哈希碰撞导致的误判。但是，哈希函数的数量不能无限制增加，因为这会带来额外的计算开销，并可能导致性能下降。因此，需要在误判率和性能之间做出权衡。

控制输入数据总量也非常重要。保持实际处理的对象数不超过设计之初预估的最大容量非常重要。因为一旦超过了最初设定范围内的估计值，则会不可避免地引起更高的失误几率；因此合理规划并严格控制进入过滤层之前的数据流至关重要。

布隆过滤器的应用场景

布隆过滤器在许多领域得到了广泛的应用。在网页爬虫中，它可以用来对URL进行去重，避免重复爬取相同的页面。在垃圾邮件识别中，它可以快速判断一封邮件是否可能是垃圾邮件，减少不必要的处理和过滤。在数据库查询中，它可以快速判断某个