布隆过滤器原理,高效空间利用与概率性数据结构原理解析

你有没有想过，在浩瀚的数据海洋中，如何快速判断一个元素是否存在于某个集合里？传统的哈希表虽然查询速度快，但随着数据量的增长，内存消耗会急剧上升。这时，布隆过滤器原理就闪亮登场了。它是一种空间效率极高的概率型数据结构，能在极小的空间内完成元素的快速检索，同时保持较低的误判率。今天，就让我们一起深入探索布隆过滤器的奥秘，看看它是如何做到既节省空间又快速判断的。

布隆过滤器的核心组成

布隆过滤器主要由两部分组成：一个位数组和一系列哈希函数。位数组是一个由0和1组成的数组，初始时所有位都设置为0。哈希函数则是一系列将输入映射到位数组特定位置的函数。通常，布隆过滤器会使用多个哈希函数（k个），以确保元素的插入和查询更加均匀和高效。

想象你有一个巨大的图书馆，需要快速判断一本书是否已经存在。布隆过滤器就像一个超级图书管理员，它不会存储书的内容，而是通过书的ISBN号（相当于元素的哈希值）快速定位到书架上的某个位置。如果这个位置的书架上有书，就说明这本书可能存在；如果书架是空的，那这本书一定不存在。

布隆过滤器的插入过程

当你向布隆过滤器中插入一个新元素时，这个过程其实非常简单。首先，你需要使用k个哈希函数对元素进行计算，得到k个哈希值。每个哈希值都会映射到位数组上的一个特定位置。将这些位置对应的位都设置为1。这样，经过多次插入操作后，部分或全部位可能会被置为1。

举个例子，假设你有一个长度为100的位数组，并且使用3个哈希函数。当你插入一个元素时，这3个哈希函数会分别计算出3个不同的位置，并将这些位置的位设置为1。如果插入另一个元素，这3个哈希函数又会计算出另外3个位置，并将这些位置的位设置为1。这样，经过多次插入后，位数组中的一些位会被置为1，而另一些位则保持为0。

布隆过滤器的查询过程

查询一个元素是否在布隆过滤器中，同样需要使用k个哈希函数。这些哈希函数会计算出k个位置，然后检查这些位置的位是否都是1。如果所有这些位置的位都是1，那么布隆过滤器认为该元素可能存在于集合中；如果这些位置中有任何一个位值不为1，那么该元素肯定不在集合中。

继续上面的例子，假设你想要查询一个元素是否存在于布隆过滤器中。这3个哈希函数会计算出3个位置，然后检查这些位置的位是否都是1。如果都是1，就说明这个元素可能存在；如果有一个或多个位置是0，就说明这个元素一定不存在。

布隆过滤器的误判率

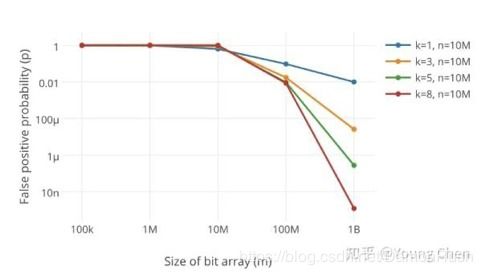
布隆过滤器的一个主要缺点是存在一定的误判率，即可能会将不在集合中的元素误判为在集合中。这是由于不同元素的哈希值可能会产生冲突，导致位数组中的某些位被错误地置为1。不过，通过合理选择哈希函数的个数和位数组的大小，可以控制误判率在一个较低的水平。

误判率与位数组的长度m、哈希函数的个数k以及布隆过滤器中存入的数据量n有关。当m增大、k增大、n减小时，误判率会降低。因此，在实际应用中，需要根据具体需求调整这些参数，以平衡空间效率和误判率。

布隆过滤器的应用场景

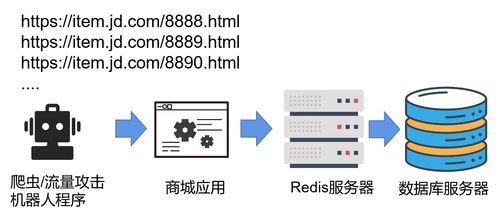
布隆过滤器原理在许多领域都有广泛的应用，其中最典型的场景之一是防止缓存穿透。在缓存系统中，布隆过滤器可以在查询缓存之前快速判断一个数据是否存在，从而避免大量不存在的数据直接穿透缓存访问数据库，减轻数据库的压力。

举个例子，假设你有一个电商网站，用户经常查询一些不存在的商品。如果没有布隆过滤器，每次查询都会直接访问数据库，给数据库带来很大压力。而有了布隆过滤器，可以在查询缓存之前快速判断一个商品是否存在，如果不存在，就直接拦截，从而减少数据库的压力。

此外，布隆过滤器原理还可以用于黑名单过滤、垃圾邮件过滤等领域。在这些场景中，布隆过滤器能够快速判断一个元素是否存在于某个集合中，从而提高系统的效率和准确性。

布隆过滤器的优缺点

布隆过滤器原理的优点主要体现在以下几个方面：

1. 空间效率高：相比于传统的数据结构（如哈希表），布隆过滤器在存储大规模数据时占用的空间要小得多。因为它只需要一个位数组来存储数据的特征，而不需要存储数据本身。

2. 查询速度快：查询操作的时间复杂度为O(k)，其中k为哈希函数的个数。这意味着即使数据量非常大，查询